Aperçu des procédures de chiffrement
Le chiffrement est une méthode permettant de traduire, à l’aide d’une clé, du texte brut en une chaîne de caractères incompréhensible. Dans le meilleur des cas, le contenu du chiffrement ainsi obtenu n’est accessible qu’à ceux qui peuvent défaire le chiffrement à l’aide de la clé. Les termes « plaintext » et « cryptogramme » peuvent être considérés comme des développements historiques. En plus des messages texte, les techniques modernes de chiffrement peuvent également être appliquées à d’autres informations électroniques, comme les messages vocaux, les fichiers images ou le code d’un programme.
Le chiffrement est utilisé pour protéger les fichiers, lecteurs ou répertoires contre un accès non désiré, ou pour transmettre confidentiellement des données. Même dans l’Antiquité, on utilisait des méthodes de chiffrement simples, qui se limitaient principalement au codage de l’information à protéger. Les caractères individuels du texte en clair, des mots ou des phrases entières du message sont alors réarrangés (transposition) ou remplacés par d’autres combinaisons de caractères (substitution).
Pour décoder un texte chiffré, le destinataire doit connaître la règle selon laquelle le texte a été encodé. Les permutations dans le cadre des procédures de transposition sont généralement effectuées à l’aide d’une matrice. Pour pouvoir réécrire un chiffrement en texte clair, la matrice de transposition doit être connue ou bien reconstruite. Les procédures de substitution sont basées sur une assignation tabulaire de caractères et de chiffres en clair, sous la forme d’un livre-code secret.
L’une des premières méthodes de chiffrement de ce type remonte à Jules César. Le chiffrement César est basé sur la substitution mono alphabétique. Pour protéger sa correspondance militaire contre les espions ennemis, le commandant avisé a décalé les lettres de ses mots de trois rangs dans l’alphabet. Le résultat se présentait ainsi :
Le nombre d’étapes par lesquelles les caractères sont décalés peut être considéré comme une clé dans ce type de chiffrement. Ce n’est pas un chiffre, mais la lettre correspondante dans l’alphabet. Un décalage de trois chiffres correspond à la touche « C ».
Alors que le chiffre de César (chiffrement par décalage) est relativement facile à comprendre, les chiffrements modernes reposent aujourd’hui sur des fonctions mathématiques plus complexes, appelées algorithmes, qui combinent plusieurs substitutions et transmutations, et sont paramétrées par des clés sous forme de mots de passe ou de codes binaires. Pour les cryptoanalyseurs (code crackers), ces méthodes présentent des obstacles beaucoup plus importants. De nombreux cryptosystèmes établis sont considérés comme incassables par les moyens disponibles aujourd’hui.
Comment fonctionne le chiffrement ?
Une méthode de chiffrement repose essentiellement sur deux composants : un algorithme cryptographique et au moins une clé secrète. Alors que l’algorithme décrit la méthode de chiffrement (par exemple « déplacer chaque lettre dans la séquence de l’alphabet »), la clé renvoie les paramètres (par exemple « C = trois rangs »). Le chiffrement peut donc être décrit comme un processus dans lequel un algorithme cryptographique reçoit le texte en clair et une clé, dont il résulte un chiffrement.
Clé digitale
Dans les méthodes modernes de chiffrement, on utilise des clés numériques sous forme de séquences de bits. Un critère essentiel pour la sécurité du chiffrement est la longueur de clé en bits. Ceci spécifie la mesure logarithmique pour le nombre de combinaisons de touches possibles. C’est ce qu’on appelle aussi la salle des clés. Plus l’espace clé est grand, plus il est résistant aux attaques de force brute, une méthode de déchiffrement basée sur l’essai de toutes les combinaisons possibles.
Les codes en chiffrement de César attaqués par force brute peuvent être décryptés. Leur espace de clé est de 25, ce qui correspond à une longueur de clé inférieure à 5 bits. Un codecracker n’a qu’à essayer 25 combinaisons pour déchiffrer le texte en clair. Le chiffrement de César n’est donc pas un obstacle sérieux. Les méthodes modernes de chiffrement, d’autre part, utilisent des clés qui peuvent représenter beaucoup plus d’états. La norme Advanced Encryption Standard (AES), par exemple, offre la possibilité de sélectionner des longueurs de clé de 128, 192 ou 256 bits. L’espace clé de cette procédure est donc important.
Même avec un chiffrement 128 bits, 2128 situations peuvent être représentées. Cela correspond à plus de 340 sextillions de combinaisons de touches possibles. Si AES fonctionne avec 256 bits, le nombre de clés possibles est supérieur à 115 duodécilliards. Même avec un équipement technique approprié, il faudrait une éternité pour essayer toutes les combinaisons possibles. Avec la technologie disponible aujourd’hui, les attaques par force brute ne sont donc pas réalisables sur la salle des clés AES.
Le principe de Kerckhoffs
En raison des longueurs de clé communes, les attaques par force brute pour les méthodes modernes de chiffrement ne sont plus une menace. Les codebreakers recherchent plutôt des faiblesses dans l’algorithme, ce qui permet de réduire le temps de calcul pour déchiffrer les données chiffrées. Une autre approche se concentre sur ce qu’on appelle les attaques de canaux latéraux, qui visent la mise en œuvre d’un cryptosystème dans un dispositif ou un logiciel. Le secret d’une procédure de chiffrement est plutôt contre-productif pour sa sécurité.
Selon le principe de Kerckhoff, la sécurité d’un cryptosystème ne repose pas sur le secret de l’algorithme, mais sur celui de la clé. Dès 1883, Auguste Kerckhoffs a formulé l’un des principes de la cryptographie moderne : afin de chiffrer un texte clair de manière fiable, il suffit de fournir une procédure mathématique bien connue, bien décrite, avec des paramètres secrets. Cette hypothèse est globalement restée intacte à ce jour.
Comme beaucoup d’autres domaines de l’ingénierie logicielle, le développement des mécanismes de chiffrement repose sur l’hypothèse que l’open source ne compromet pas la sécurité. Au contraire, une application conséquente du principe de Kerckhoff conduit à une détection plus rapide des erreurs dans les algorithmes cryptographiques, puisque les méthodes correspondantes doivent résister aux regards critiques des experts.
Expansion de clé : du mot de passe à la clé
Les utilisateurs qui veulent chiffrer ou déchiffrer des données n’entrent généralement pas en contact avec les clés, mais utilisent une chaîne de caractères plus maniable : le mot de passe. Les mots de passe sécurisés contiennent 8 à 12 caractères combinant lettres, chiffres et caractères spéciaux, et présentent un avantage décisif sur les séquences de bits, puisque les utilisateurs peuvent directement s’en souvenir.
Cependant, les mots de passe ne conviennent pas comme clés dans le contexte du chiffrement, en raison de leur longueur réduite. De nombreuses méthodes de chiffrement contiennent donc une étape intermédiaire dans laquelle un mot de passe de n’importe quelle longueur est converti en une séquence de bits fixe correspondant au système de chiffrement. Il existe par ailleurs des méthodes dans lesquelles les clés sont générées au hasard, dans la limite des possibilités techniques.
PBKDF2 (Password-Based Key Derivation Function 2) est une méthode courante pour calculer les clés à partir des mots de passe. Dans le cadre de cette procédure, les mots de passe sont complétés par une chaîne de caractères pseudo-aléatoires, le salage, et ensuite mappés en séquences binaires de la longueur désirée, à l’aide de fonctions de hashtags cryptographiques.
Les fonctions de hachage sont des fonctions antichoc unidirectionnelles, c’est-à-dire des calculs relativement faciles en soit, mais qui ne peuvent être inversés que difficilement. En cryptographie, une procédure est dite sécurisée si différents hachages sont affectés à différents documents. Les mots de passe qui ont été convertis en clés grâce à des fonctions unidirectionnelles ne peuvent être reconstitués qu’avec un effort de calcul considérable. Ceci est similaire à une recherche dans l’annuaire téléphonique : s’il est facile de trouver le bon numéro de téléphone pour un nom donné, la recherche d’un nom par numéro de téléphone peut devenir un problème insoluble.
Le calcul mathématique est effectué dans le cadre de PBKDF2 en plusieurs itérations (répétitions) pour protéger la clé ainsi générée contre les attaques de force brute. La valeur de sel augmente l’effort pour la reconstruction d’un mot de passe basé sur des tables arc-en-ciel. C’est un schéma d’attaque dans lequel les codeurs utilisent des valeurs de hachage stockées pour identifier un mot de passe inconnu.
Il existe d’autres méthodes de hachage de mot de passe comme scrypt, bcrypt et LM hash. Toutefois, cette dernière est considérée comme obsolète et incertaine.
Le problème de distribution de clés
L’un des problèmes principaux en cryptologie réside dans le fait de savoir comment les informations peuvent être chiffrées à un endroit et en clair à un autre. Jules César était déjà confronté au problème de la distribution des clés. Si le commandant voulait envoyer un message chiffré de Rome au front germanique, il devait s’assurer que le destinataire était capable de déchiffrer le message secret. La seule solution était de transmettre par un messager non seulement le texte secret, mais aussi la clé. Mais comment la clé peut-elle être remise sans risquer de tomber entre les mains de ces tiers ?
C’est la même question qui préoccupe encore aujourd’hui les cryptologues lorsqu’il s’agit de transmettre des données chiffrées sur Internet. Des suggestions de solutions ont été incorporées dans le développement de divers cryptosystèmes et protocoles d’échange de clés. Le problème de distribution clé des cryptosystèmes symétriques peut être considéré comme la principale motivation du développement des méthodes de chiffrement asymétrique.
Vers la classification des méthodes de chiffrement
Dans la cryptologie moderne, une distinction fondamentale est faite entre les méthodes de chiffrement symétrique et asymétrique. La classification est basée sur la manipulation des clés.
Pour les cryptosystèmes symétriques, la même clé est utilisée pour le chiffrement et le déchiffrement des données chiffrées. Si deux parties communicantes veulent échanger des données chiffrées, il faut trouver un moyen de transmettre secrètement la clé partagée. Dans les cryptosystèmes asymétriques, par contre, chaque partenaire de communication génère sa propre paire de clés : une clé publique et une clé privée.
Si des méthodes de chiffrement symétrique et asymétrique sont utilisées en combinaison, on les appelle des méthodes hybrides.
Méthodes de chiffrement symétrique
Jusqu’aux années 1970, le chiffrement de l’information était basé sur des cryptosystèmes symétriques dont les origines remontent à des méthodes anciennes comme le chiffrement de César. Le principe de base du chiffrement symétrique est que le chiffrement et le déchiffrement se font à l’aide de la même clé. Si deux parties veulent communiquer de façon chiffrée, l’expéditeur et le destinataire doivent avoir une copie de la clé commune. Afin de protéger les informations chiffrées contre l’accès par des tiers, la clé symétrique est gardée secrète. Il s’agit donc également d’une procédure de clé privée.
Alors que les méthodes de chiffrement symétrique classiques fonctionnent au niveau de la lettre pour convertir du texte brut en textes secrets, le chiffrement se fait au niveau du bit dans les systèmes de chiffrement assistés par ordinateur. On distingue le chiffrement de puissance du chiffrement de bloc :
- Chiffrement de puissance : chaque caractère ou bit du texte en clair est lié à un caractère ou bit du flux de clés, et ainsi traduit en un caractère de sortie chiffré.
- Chiffrement de bloc : les caractères ou bits à chiffrer sont combinés en blocs de longueur fixe et mappés sur un chiffrement de longueur fixe.
Les méthodes courantes de chiffrement des cryptosystèmes symétriques sont des opérations relativement simples, telles que les substitutions et les transpositions, qui sont combinées dans des méthodes modernes et appliquées au texte simple en plusieurs cycles successifs (itérations). De plus, les additions, les multiplications, les opérations arithmétiques modulaires et les opérations XOR sont intégrées dans des algorithmes de chiffrement symétriques modernes.
Les méthodes de chiffrement symétrique bien connues sont la norme de chiffrement des données (DES) désormais obsolète et son successeur, l’Advanced Encryption Standard (AES).
Data Encryption Standard (DES)
DES est une méthode de chiffrement symétrique développée par IBM dans les années 1970 et normalisée en 1977 par le National Institute of Standards and Technology (NIST) nord-américain. DES est la première méthode de chiffrement assistée par ordinateur pour établir les débuts de la cryptographie moderne. La norme est libre de droits de brevet, mais en raison de la petite longueur de clé de 64 bits (actuellement seulement 56 bits), elle est maintenant considérée comme obsolète. Dès 1994, le cryptosystème était divisé avec douze stations de travail HP-9735 et un temps de calcul de 50 jours. Grâce à la technologie de pointe actuelle, une clé DES peut être déchiffrée en quelques heures par des attaques de force brute.
L’algorithme symétrique fonctionne comme un chiffrement bloc au niveau du bit. Le texte brut est divisé en blocs de 64 bits, qui sont encodés individuellement avec une clé 64 bits. Ainsi, le texte brut 64 bits est traduit en texte codé 64 bits. Comme chaque huitième bit de la clé agit comme un bit de parité, seuls 56 bits sont effectivement disponibles pour le chiffrement.
L’algorithme de chiffrement DES est un réseau de Feistel, basé sur une combinaison de substitutions et de transpositions, qui sont effectuées en 16 itérations. La procédure, qui porte le nom de l’employé d’IBM Horst Feistel, peut être décrite en quatre étapes :
- Permutation d’entrée : le bloc de texte 64 bits est soumis à une permutation d’entrée qui change la séquence des bits. Le résultat de cette permutation est écrit sur deux registres 32 bits. Sont ainsi créés un demi-bloc gauche (L) et un demi-bloc droit (R).
- Permutation des clés : les 56 bits de la clé qui sont importants pour le chiffrement sont également soumis à une permutation et sont ensuite divisés en deux blocs de 28 bits (C et D). Une clé ronde est générée à partir des deux blocs de touches C et D pour chacune des 16 itérations. Pour cela, les bits des deux demi-blocs sont décalés cycliquement de 1 ou 2 bits vers la gauche. Ceci permet de s’assurer qu’une clé ronde différente est incluse dans chaque cycle de chiffrement. Les deux demi-blocs C et D sont ensuite mappés sur une clé ronde de 48 bits.
- Rondes de chiffrement : chaque cycle de chiffrement comprend les étapes a) à d). Un demi-bloc R et une clé ronde sont utilisés pour chaque boucle dans le chiffrement. Le demi-bloc L est d’abord omis.
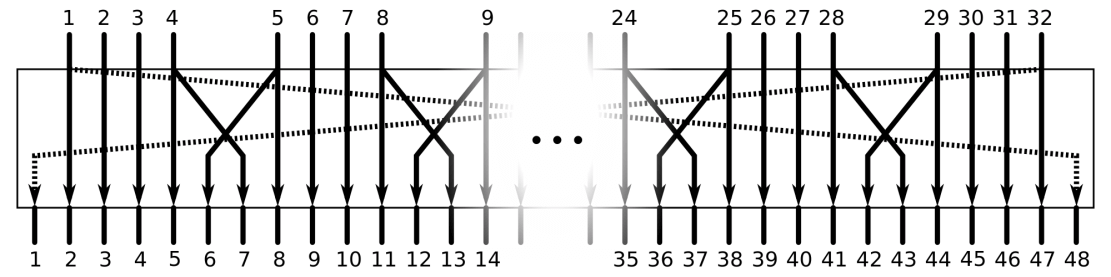
- Expansion : le demi-bloc R est étendu à un bloc 48 bits par expansion. À cette fin, les 32 bits du demi-bloc sont divisés en groupes de 4 bits dans le cadre de l’expansion, puis partiellement dupliqués et permutés selon le schéma suivant :
- Connexion XOR d’un bloc de données et d’une clé ronde : dans chaque cycle de chiffrement, le bloc 48 bits R étendu est relié à une clé ronde de 48 bits au moyen d’une opération XOR. Le résultat de l’opération XOR est à nouveau un bloc de 48 bits.
- Boîtes S (boîtes de substitution) : après la liaison XOR, le bloc 48 bits est divisé en huit blocs 6 bits, remplacé par huit blocs 4 bits à l’aide de S-Box et combiné en un bloc 32 bits. Le résultat des cases de substitution est à nouveau soumis à une permutation.
- Combinaison XOR de R-Block et L-Block : après chaque cycle de chiffrement, le résultat des S-Boxes est lié au L-Block précédemment inutilisé à l’aide de XOR. Le résultat est un bloc 32 bits qui entre dans le deuxième cycle de chiffrement comme un nouveau bloc R. Le bloc R du premier tour est utilisé comme bloc L du deuxième tour.
- Permutation de sortie : si les 16 rondes de chiffrement ont été exécutées, les blocs L et R sont combinés en un bloc 64 bits et soumis à une permutation de sortie inversée à la permutation d’entrée. Le texte clair est maintenant chiffré.
Le diagramme suivant montre une représentation schématique de l’algorithme DES. Les liens XOR sont marqués comme des cercles rouges avec des croix blanches.
Le déchiffrement d’un texte secret chiffré par DES suit le même schéma dans l’ordre inverse.
L’une des principales critiques à DES est la faible longueur de clé de 56 bits, ce qui se traduit par un espace de clé relativement petit. Ceci ne résiste plus aux attaques de force brute avec la puissance de calcul disponible aujourd’hui. En outre, la méthode de permutation des clés, qui produit 16 touches rondes presque identiques, est considérée comme trop faible.
Avec Triple-DES (3DES), une variante de DES a été développée, dans laquelle le processus de chiffrement est exécuté en trois cycles consécutifs. Cependant, la longueur de clé effective de 3DES n’est que de 112 bits, ce qui reste inférieur à la norme minimale actuelle de 128 bits. De plus, 3DES est nettement plus gourmand en calcul que DES.
La norme de chiffrement des données a donc été largement remplacée. L’algorithme de chiffrement également symétrique Advanced Encryption Standard est considéré comme le successeur.
Advanced Encryption Standard (AES)
Dans les années 1990, il est devenu évident que la norme de chiffrement DES la plus fréquemment utilisée n’était plus en mesure de faire face aux évolutions techniques. Une nouvelle norme de chiffrement était nécessaire. Le successeur de l’algorithme de Rijndael, nommé d’après le nom de ses développeurs Vincent Rijmen et Joan Daemen (débat: « Reindahl »), s’est imposé comme le successeur - une procédure qui a été acceptée dans un appel d’offres public pour sa sécurité, sa flexibilité et ses performances et qui a été certifiée par le NIST en tant que norme de chiffrement avancée (AES) à la fin de l’année 2000.
AES divise également le texte brut à chiffrer en blocs. Ainsi, ce cryptosystème est, à l’instar de DES, basé sur le chiffrement de bloc. La norme prend en charge les clés 128, 192 et 256 bits. Cependant, au lieu de blocs 64 bits, AES utilise des blocs beaucoup plus grands de 128 bits qui sont encodés en plusieurs cycles consécutifs, à l’aide d’un réseau de permutation de substitution (SPN). Le successeur DES utilise également une nouvelle clé ronde pour chaque cycle de chiffrement, qui est dérivée récursivement de la clé initiale et liée au bloc de données à chiffrer en utilisant XOR. Le processus de chiffrement peut être divisé en quatre étapes :
- Expansion des clés : comme DES, AES utilise une nouvelle clé ronde dans chaque boucle de chiffrement. Ceci est dérivé de la clé initiale par récursion. La clé initiale est étendue à une longueur qui vous permet de mapper le nombre requis de touches rondes de 128 bits. Chaque clé ronde est donc basée sur une sous-section de la clé initiale étendue. Le nombre de touches rondes nécessaires est le nombre de tours de chiffrement (R) y compris le tour final plus une touche ronde pour le tour préliminaire (nombre de touches rondes = R + 1).
- Phase préliminaire : lors de la ronde préliminaire, le bloc d’entrée 128 bits est transféré dans une table bidimensionnelle (tableau) et relié à la première clé ronde à l’aide de XOR (KeyAddition). Le tableau contient 4 lignes et 4 colonnes. Chaque cellule contient donc un octet (8 bits) du bloc à chiffrer.
- Rondes de chiffrement : le nombre de rondes de chiffrement dépend de la longueur de clé utilisée : 10 rondes pour AES128, 12 rondes pour AES192 et 14 rondes pour AES256 :
- Sous-octets : les sous-octets sont une substitution monoalphabétique. Chaque octet du bloc à chiffrer est remplacé par un équivalent en utilisant une S-Box.
- Les rangées de quarts : dans le contexte de la transformation ShiftRow, les octets dans les cellules du réseau (voir le tour préliminaire) sont déplacés cycliquement vers la gauche.
- MixColumns : avec MixColumns, l’algorithme AES inclut une transformation dans laquelle les données sont fusionnées dans les colonnes du tableau. Cette étape est basée sur un nouveau calcul de chaque cellule individuelle. Pour cela, les colonnes de la matrice sont soumises à une multiplication matricielle et les résultats sont liés par XOR.
- KeyAddition : à la fin de chaque cycle de chiffrement, un autre KeyAddition a lieu. Comme dans le tour préliminaire, il est basé sur un lien XOR entre le bloc de données et la touche ronde courante.
- Final Round : le dernier round est le dernier round de chiffrement. Contrairement aux cycles précédents, il ne contient pas de transformations MixColumns et ne comprend donc que les opérations SubBytes, ShiftRows et KeyAddition. Le résultat du dernier tour est le texte secret.
Le déchiffrement des données chiffrées AES est basé sur l’investissement de l’algorithme de chiffrement. En plus de la séquence d’étapes, ceci se réfère également aux opérations ShiftRow, MixColumns et SubBytes, dont la direction est également inversée.
AES est certifié hautement sécurisé grâce à son algorithme. À ce jour, aucune attaque pratique n’est connue. Les attaques par force brute sont inefficaces en raison de la longueur de clé d’au moins 128 bits. De plus, des opérations telles que ShiftRows et MixColumns garantissent un mixage optimal des bits : dans le résultat, chaque bit dépend de la clé. De plus, le cryptosystème convainc par sa simplicité d’implémentation et sa grande vitesse. AES est utilisé comme norme de chiffrement pour WPA2, SSH et IPSec ainsi que comme algorithme de chiffrement pour les archives de fichiers compressés telles que 7-Zip ou RAR.
Cependant, les données chiffrées AES ne sont protégées contre l’accès par des tiers que si la clé reste secrète. Comme la même clé est utilisée pour le chiffrement et le déchiffrement, le cryptosystème est affecté par le problème de distribution des clés comme toute autre méthode symétrique. L’utilisation en toute sécurité d’AES est donc limitée aux domaines d’application qui ne nécessitent pas d’échange de clés ou qui le permettent via un canal sécurisé.
Toutefois, la communication chiffrée sur Internet exige que les données soient chiffrées sur un ordinateur et déchiffrées sur un autre. Ici, des cryptosystèmes asymétriques se sont installés, qui permettent un échange sécurisé de clés symétriques ou de fonctions sans l’échange d’une clé commune.
Les cryptosystèmes symétriques MARS, RC6, Serpent et Twofish, qui sont également basés sur le chiffrement par blocs et ont été parmi les finalistes de l’appel d’offres AES, offrent une alternative à AES. Le prédécesseur de deux poissons, Blowfish, est toujours utilisé. Le système de chiffrement électrique Salsa20, développé en 2005 par Daniel J. Bernstein, figure parmi les finalistes du projet européen eSTREAM.
Méthodes de chiffrement asymétrique
Alors que la même clé est utilisée pour les cryptosystèmes symétriques des deux côtés de la communication chiffrée, les deux parties d’une communication chiffrée asymétrique génèrent une paire de clés par côté. Chaque abonné de communication dispose ainsi de deux clés : une clé publique et une clé privée. Pour communiquer sous forme chiffrée, chaque partie doit divulguer sa clé publique. Ceci se fait généralement via des serveurs clés. C’est ce qu’on appelle une procédure à clé publique. La clé privée, en revanche, reste secrète. Ceci montre la force des cryptosystèmes asymétriques : contrairement au chiffrement symétrique, la clé secrète n’est jamais donnée hors de contrôle à aucun moment.
Dans le contexte du chiffrement asymétrique, les clés publiques sont utilisées pour le chiffrement. Ils permettent également de vérifier les signatures numériques et les utilisateurs. Les clés privées, quant à elles, sont utilisées pour le déchiffrement et permettent de générer des signatures numériques ou de s’authentifier contre d’autres utilisateurs.
Voici un exemple :
L’utilisateur A souhaite que l’utilisateur B envoie un message chiffré. La clé publique de B permet à A de chiffrer un message de telle sorte qu’il ne peut être déchiffré qu’avec la clé privée de B. La clé publique de B permet à A de déchiffrer un message de telle sorte qu’il ne peut être déchiffré qu’avec la clé privée de B. La clé publique de B permet à A de déchiffrer un message de telle sorte qu’il ne peut être déchiffré qu’avec la clé privée de B. A part B, personne n’est capable de lire le message. Même A n’a aucun moyen de déchiffrer le message après chiffrement.
L’avantage du chiffrement asymétrique est que tout le monde peut utiliser la clé publique de l’utilisateur B pour chiffrer les messages, mais que seul B peut les déchiffrer avec sa clé secrète. Étant donné que seule la clé publique est échangée, il n’est pas nécessaire d’utiliser un canal protégé contre les effractions.
L’un des inconvénients de cette méthode de chiffrement, cependant, est que B ne peut pas être sûr que le message chiffré provient bien de A. En principe, un tiers (C) pourrait également utiliser la clé publique de B pour chiffrer les messages, par exemple, pour propager des logiciels malveillants. De plus, A ne peut pas être sûr qu’une clé publique est bien la clé de B. C pourrait également créer une clé publique et l’utiliser comme la clé de B pour intercepter les messages de A à B. Dans le cadre du chiffrement asymétrique, un mécanisme est donc nécessaire pour qu’un partenaire de communication puisse vérifier l’authenticité de l’autre.
Les certificats et signatures numériques peuvent résoudre ce problème.
- Certificats numériques : afin de sécuriser les procédures de chiffrement asymétrique, les partenaires de communication ont la possibilité de faire authentifier leurs clés publiques par une autorité de certification officielle. Un standard commun pour les certificats de clés publiques est X. 509, qui est utilisé pour la transmission de données chiffrées TLS/SSL via HTTPS ou dans le cadre du chiffrement des e-mails via S/MIME, par exemple.
- Signatures numériques : alors que les certificats numériques sont utilisés pour vérifier les clés publiques, les signatures numériques sont utilisées pour identifier sans équivoque l’expéditeur d’un message chiffré. Pour ce faire, il utilise sa clé privée pour générer une signature. Le destinataire vérifie ensuite cette signature à l’aide de la clé publique de l’expéditeur. L’authenticité des signatures numériques peut être garantie par des infrastructures à clé publique (ICP) hiérarchiquement structurées. Le système DE-Mail en est un exemple. Une alternative décentralisée à l’ICP hiérarchique est le Web of Trust (WOT), un réseau dans lequel les utilisateurs se vérifient directement et indirectement.
La première publication d’une méthode de chiffrement asymétrique date de 1977, par les mathématiciens Rivest, Shamir et Adleman. La procédure RSA nommée d’après les inventeurs est basée sur des fonctions jetables avec trappe et peut être utilisée pour le chiffrement des données ainsi que les procédures de signature.
Rivest, Shamir, Adleman (RSA)
Le chiffrement RSA est considéré comme l’une des procédures de clé publique les plus sûres et les mieux décrites. L’idée de chiffrer en utilisant une clé de chiffrement publique et une clé de déchiffrement secrète est basée sur les cryptologues Whitfield Diffie et Martin Hellman. Publiées en 1976, avec l’échange de clés Diffie-Hellman, elles permettent à deux partenaires de communication de s’accorder sur une clé secrète via un canal non sécurisé. Les chercheurs se sont appuyés sur le puzzle Merkles développé par Ralph Merkle. C’est ce qu’on appelle aussi l’échange de clés Diffie-Hellman-Merkle (DHM).
Les cryptogènes utilisaient des fonctions mathématiques unidirectionnelles, faciles à exécuter mais qui ne peuvent être inversées, là encore, très difficilement. Aujourd’hui encore, l’échange de clés qui porte leur nom est toujours utilisé pour négocier des clés secrètes dans les cryptosystèmes symétriques. Le concept de la trappe est un autre mérite du duo de recherche. Dans la publication de l’échange de clés Diffie-Hellman, des abréviations cachées sont déjà mentionnées : elles devraient permettre d’accélérer l’inversion d’une fonction unidirectionnelle. Diffie et Hellmann n’ont fourni aucune preuve concrète, mais leur théorie de la trappe a encouragé de nombreux cryptologues à mener leurs propres enquêtes.
Rivest, Shamir et Adleman ont également cherché des abréviations pour les fonctions à sens unique, à l’origine avec l’objectif de réfuter la théorie de la trappe porte. Cependant, leurs recherches se sont développées dans une direction différente et ont abouti à la méthode de chiffrement qui a finalement été nommée d’après eux. Aujourd’hui, RSA est considéré comme le premier algorithme, publié scientifiquement, qui permet la transmission de données chiffrées sans échange de clé secrète.
Le chiffrement RSA utilise un algorithme basé sur la multiplication de grands nombres premiers. Bien qu’il n’y ait généralement pas de problème à multiplier deux nombres premiers par 100, 200 ou 300 chiffres, il n’y a toujours pas d’algorithme efficace capable de décomposer le résultat d’une telle opération de calcul en ses facteurs premiers dans l’étape inverse. La factorisation en nombres premiers peut être illustrée par l’exemple ci-dessous.
Si vous multipliez les nombres premiers 14.629 et 30.491, vous obtenez le produit 446.052.839, qui n’a que quatre diviseurs : 1, lui-même et les deux nombres premiers qui ont été multipliés. Si vous supprimez les deux premiers diviseurs, puisque chaque nombre est divisible par 1 et par lui-même, vous obtenez les valeurs initiales 14.629 et 30.491.
Ce schéma est la base de la génération des clés RSA. Les clés publiques et privées représentent deux paires de nombres :
- Clé publique : (e, N)
- Clé privée : (d, N)
N est le module RSA. Ceci est contenu dans les deux clés et les résultats du produit de deux nombres premiers très grands p et q (N = p x q) sélectionnés au hasard.
Pour générer la clé publique, vous avez également besoin de e, un nombre qui est choisi au hasard avec certaines restrictions. Si vous combinez N et e, vous obtenez la clé publique accessible à chaque abonné de communication en texte clair.
Pour générer la clé privée, N et d sont nécessaires. d est une valeur résultant des nombres premiers p et q générés aléatoirement ainsi que du nombre aléatoire e, qui sont calculés sur la base de la fonction phi d’Euler (φ).
Les nombres premiers inclus dans le calcul de la clé privée doivent être tenus secrets afin de garantir la sécurité du chiffrement RSA. Le produit des deux nombres premiers, d’autre part, peut être utilisé en texte clair dans la clé publique, puisqu’il est supposé qu’il n’y a pas d’algorithme efficace aujourd’hui qui peut décomposer le produit de nombres premiers très grands en ses facteurs dans le temps pertinent. Il n’est donc pas possible de calculer p et q à partir de N. Sauf si vous pouvez raccourcir le calcul. Une telle trappe représente la valeur d, qui n’est connue que du propriétaire de la clé privée.
La sécurité de l’algorithme RSA dépend fortement du progrès technique. La puissance de calcul des ordinateurs double tous les deux ans. Il n’est donc pas exclu qu’une méthode efficace de factorisation primaire soit disponible dans un avenir prévisible à l’échelle habituelle. Dans ce cas, RSA offre la possibilité d’adapter l’algorithme au développement technique en utilisant des nombres premiers encore plus grands pour calculer les clés.
Procédures d'identification par pièces d'identité à clé publique
La faiblesse centrale des systèmes de chiffrement asymétrique est l’authentification des utilisateurs. Dans les procédures traditionnelles de clés publiques, une clé publique n’a aucun lien avec l’identité de son utilisateur. Si une tierce partie est capable de se faire passer pour l’une des parties impliquées dans la transmission de données chiffrées au moyen de sa propre clé publique, l’ensemble du système de chiffrement peut être exploité sans attaquer directement l’algorithme ou une clé de déchiffrement privée. Dès 1984, Adi Shamir, co-développeur de la RSA, a proposé un cryptosystème basé ID et sur l’approche asymétrique, mais qui tente de compenser sa vulnérabilité.
Dans le cadre du chiffrement basé sur l’identité (IBE), la clé publique d’un partenaire de communication n’est pas générée en fonction de la clé privée, mais calculée à partir d’un identifiant unique. Selon le contexte, il peut être approprié d’utiliser une adresse e-mail ou un domaine, par exemple. L’authentification des clés publiques par les organismes officiels de certification n’est plus nécessaire. Cependant, leur place est occupée par une autre instance : le Générateur de Clé Privée (PKG). Il s’agit d’un algorithme central qui permet d’attribuer au destinataire d’un message chiffré une clé de déchiffrement associée à son identité.
La théorie du chiffrement basé sur l’ID résout donc un problème fondamental des cryptosystèmes asymétriques, mais introduit deux autres lacunes de sécurité : un point central de la critique se pose de la question de savoir comment la clé de déchiffrement privée doit être transférée du PKG au destinataire du message chiffré. C’est là que se pose le problème bien connu de la distribution des clés. Un autre inconvénient des méthodes basées sur l’ID est le fait qu’avec le PKG, il existe une instance supplémentaire qui reconnaît la clé de déchiffrement en plus du destinataire d’un message chiffré. Il ne s’agit donc pas par définition d’une clé privée et elle peut donc être utilisée à mauvais escient. Théoriquement, le PKG a la possibilité de déchiffrer tous les messages sans autorisation. Ceci peut être évité en générant la paire de clés avec un logiciel open source sur votre propre ordinateur.
La méthode ID la plus connue est basée sur Dan Boneh et Matthew K. Franklin.
Méthode hybride
Le chiffrement hybride est la connexion entre les systèmes cryptographiques symétriques et asymétriques dans le contexte de la transmission de données sur Internet. L’objectif de cette combinaison est de compenser les faiblesses d’un système par les forces de l’autre.
Les cryptosystèmes cryptographiques symétriques tels qu’AES (Advanced Encryption Standard) sont considérés comme sécurisés dans l’état actuel de la technique et permettent de traiter rapidement et efficacement même de grandes quantités de données. Cependant, la conception de l’algorithme basé sur une clé privée commune, qui doit être échangée entre le récepteur et l’expéditeur d’un message chiffré, pose le problème de la distribution des clés pour les méthodes symétriques. Ceci peut être résolu par des cryptosystèmes asymétriques. Des procédures telles que RSA sont basées sur une séparation stricte des clés publiques et privées, permettant ainsi d’éviter le transfert d’une clé privée.
Cependant, RSA offre une protection fiable contre la cryptanalyse seulement avec une longueur de clé suffisamment grande d’au moins 1 976 bits. Il en résulte de longs processus de calcul qui disqualifient l’algorithme de chiffrement et de déchiffrement de grandes quantités de données. De plus, le texte secret à transmettre après le chiffrement RSA est considérablement plus grand que le texte brut original.
Dans le chiffrement hybride, les algorithmes asymétriques ne sont donc pas utilisés pour chiffrer les données utilisateur, mais pour sécuriser la transmission d’une clé de session symétrique sur un canal public non protégé. Ceci permet de déchiffrer efficacement les chiffres chiffrés en utilisant des algorithmes symétriques.
Le processus de chiffrement hybride peut être décrit en trois étapes :
- Gestion des clés : dans les méthodes hybrides, le chiffrement symétrique d’un message est encadré par une méthode de chiffrement asymétrique. Pour cela, il faut générer à la fois des touches asymétriques (a) et symétriques (b) :
- Avant la transmission des données chiffrées, les deux partenaires de communication génèrent une paire de clés asymétrique : une clé publique et une clé privée. Par la suite, les clés publiques sont échangées et sécurisées au mieux par un mécanisme d’authentification. La paire de clés asymétriques est utilisée pour chiffrer et déchiffrer une clé de session symétrique et est généralement utilisée plusieurs fois.
- Le chiffrement et le déchiffrement du texte clair se fait à l’aide de la clé de session symétrique. Il est régénéré par l’expéditeur d’un message lors de chaque processus de chiffrement.
- Chiffrement : si un message (complet) doit être transmis de manière sécurisée sur Internet, l’expéditeur génère d’abord une clé de session symétrique avec laquelle les données utilisateur sont chiffrées. Ensuite, la clé publique du destinataire est utilisée pour chiffrer la clé de session de manière asymétrique. Les données de l’utilisateur et la clé symétrique sont ainsi disponibles sous forme chiffrée et peuvent être envoyées sans hésitation.
- Déchiffrement : si un texte secret est reçu par le destinataire avec la clé de session chiffrée, le destinataire utilise sa clé privée pour déchiffrer asymétriquement la clé de session. Ceci est ensuite utilisé pour déchiffrer les données utilisateur chiffrées symétriquement.
Selon ce schéma, une méthode de chiffrement efficace peut être mise en œuvre et même de grandes quantités de données d’utilisateur peuvent être chiffrées et déchiffrées de manière sécurisée et à grande vitesse. Puisque seule une courte clé de session est chiffrée de manière asymétrique, les temps de calcul relativement longs des algorithmes asymétriques ne sont pas pertinents pour le chiffrement hybride. Le problème de distribution des clés du chiffrement symétrique est réduit au problème de l’authentification utilisateur par le chiffrement asymétrique de la clé de session. Comme pour les systèmes cryptographiques purement asymétriques, ceci peut être résolu par des signatures numériques et des certificats.
Des méthodes de chiffrement hybrides sont utilisées sous forme d’IPSec pour la communication sécurisée sur des réseaux IP non sécurisés. Le protocole Hypertext Transfer Protocol Secure (HTTPS) repose également sur un protocole de chiffrement hybride avec TLS/SSL qui combine des systèmes de chiffrement symétrique et asymétrique. En outre, la mise en œuvre de la méthode hybride est à la base des normes de chiffrement telles que Pretty Good Privacy (PGP), GnuPG et S/MIME, qui sont utilisées dans le chiffrement des emails.
L’une des combinaisons courantes dans le chiffrement hybride est le chiffrement symétrique des données utilisateur via AES et le chiffrement asymétrique ultérieur de la clé de session via RSA. Alternativement, la clé de session peut être négociée en utilisant la méthode Diffie-Hellman. Ceci peut fournir une sécurité avancée en tant que Diffie-Hellman éphémère, mais il est vulnérable aux attaques de l’homme du milieu. Le cryptosystème Elgamal remplace l’algorithme RSA. La méthode des clés publiques développée par Taher Elgamal en 1985 est également basée sur l’idée de l’échange de clés Diffie-Hellman et est utilisée dans la version actuelle du programme de chiffrement PGP.